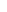Maths

Vision

Here at Hadrian Academy, we encourage children to have a ‘Mastery’ approach to mathematics, by being resilient, co-operative, creative, and most importantly, by having a positive attitude, not being afraid to make mistakes and being determined to seek solutions. We encourage all children to develop their own mathematical understanding through arithmetical proficiency, reasoning and problem-solving skills. We strive for our pupils to be confident mathematicians who understand the relevance of the subject in their everyday lives.

Aims

We aim to develop lively, enquiring minds, encouraging pupils to become self-motivated, confident and capable in solving problems. The National Curriculum for mathematics aims to ensure that all pupils:

become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils have conceptual understanding, and are able to recall and apply their knowledge rapidly and accurately;
reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language;
can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.

Five Big Ideas of Mastery

Our teaching for mastery is underpinned by the NCETM’s 5 Big Ideas:

Coherence, representation and structure, mathematical thinking, fluency and variation.

Coherence

Lessons are broken down into small connected steps that gradually unfold the concept, providing access for all children and leading to a generalisation and the ability to apply the concept to a range of contexts.

Representation and Structure

Representations used in lessons expose the mathematical structure being taught, the aim being that students can do the maths without needing the visual representation.

Mathematical Thinking

If taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned with and discussed with others.

Fluency

Quick and efficient recall of facts and procedures and the flexibility to move between different contexts and representations of mathematics.

Variation

Variation is twofold. It is firstly about how the teacher represents the concept being taught, often in more than one way, to draw attention to critical aspects, and to develop deep and holistic understanding. It is also about the sequencing of the activities and exercises used within a lesson and follow up practice, paying attention to what is kept the same and what changes, to connect the mathematics and draw attention to mathematical relationships and structure.

Lesson Structure

Each Power Maths lesson follows the same sequence and is designed to empower children to understand core concepts and grow in confidence.

Discover – each lesson begins with a problem to solve, often a real-life example, sometimes a puzzle or a game. These are engaging and fun, and designed to get all children thinking and generate curiosity. Children may use manipulatives(practical apparatus) to help them understand the maths and explain their method.
Share – the class shares their ideas and compares different ways to solve the problem, explaining their reasoning with hands-on resources and drawings to make their ideas clear. Children are able to develop their understanding of the concept with input from the teacher.
Think together – the next part of the lesson is a journey through the concept, digging deeper and deeper so that each child builds on secure foundations, while being challenged to apply their understanding in different ways and with increasing independence.
Practice – now children practise individually or in small groups, rehearsing and developing their skills to build fluency, understanding of the concept and confidence.
Reflect – finally, children are prompted to reflect on and record their learning from each session and show how they have grasped the concept explored in the lesson.

What learning looks like

Teaching the whole class together enables all children to access the learning.
Children are not ability grouped as continuous AfL is used to identify strengths and need for support.
Small focus of learning for the lesson builds on prior learning.
Learning starts with a problem to contextualise the maths and to give it a purpose.
Precise and accurate mathematical language is encouraged to be used by both adults and pupils.
Questions are planned to challenge thinking and to develop understanding.
Children are encouraged to answer in full sentences to explain their thinking.
STEM sentences are used to support learning and expose connections.
Discussion plays a key part within lessons as pupils are given time to put into words their thinking to develop their reasoning.
Concrete – Pictorial – Abstract (CPA) representations are planned carefully to ensure children can ‘see’ and therefore understand the maths rather than just following a procedure.
‘I do’, We do’, ‘You do’ approach is used to model and scaffold the learning.
Common misconceptions are addressed and planned for to draw attention to the key learning.
Conceptual variation ensures children can transfer a skill from one context to another.
Procedural variation encourages children to look for connections in their learning.
Children are actively encouraged to seek for patterns and share what they notice within their learning.
Independent learning enables children to apply their new skills and knowledge
Children who understand the learning are encouraged to go deeper within a concept with planned questions and investigations.
Children requiring support are kept with the teacher or TA for further guided practice.
Differentiation will mainly be through the level of adult support each child receives. Generally, the task for each child will be the same..

These events have previously included milkshake parties, a sweet shop and a scooter afternoon.

Maths

Vision

Aims

Lesson Structure

What learning looks like

Progression

Calculation policies

Useful Guides

Examples of Golden Pass Test